The definition of the invariant interval is
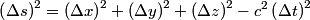 First, we evaluate 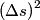 in inertial frame in inertial frame 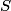 : :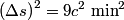 Now, we evaluate 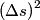 in inertial frame in inertial frame 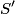 : :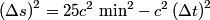 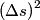 must have the same value when evaluated in the two inertial frames, therefore must have the same value when evaluated in the two inertial frames, therefore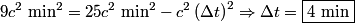 Therefore, answer (C) is correct. |
The definition of the invariant interval is
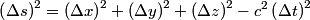 First, we evaluate 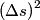 in inertial frame in inertial frame 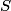 : :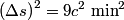 Now, we evaluate 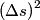 in inertial frame in inertial frame 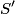 : :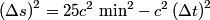 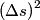 must have the same value when evaluated in the two inertial frames, therefore must have the same value when evaluated in the two inertial frames, therefore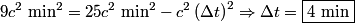 Therefore, answer (C) is correct. |